Aufgabe C 2
In einer Urne befinden sich drei rote, eine weiße und sechs schwarze Kugeln.
a) Es werden nacheinander acht Kugeln mit Zurücklegen gezogen.
Bestimmen Sie für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:
A: Genau drei dieser Kugeln sind rot.
B: Mehr als zwei und weniger als sechs dieser Kugeln sind rot.
C: Die ersten drei Kugeln haben dieselbe Farbe.
(3 VP)
b) Geben Sie im Zusammenhang mit der oben beschriebenen Urne ein Zufallsexperiment und ein Ereignis an, dessen Wahrscheinlichkeit sich mit dem folgenden Term berechnen lässt: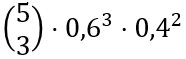
(1,5 VP)
c ) Bei einem Spiel werden zwei Kugeln ohne Zurücklegen gezogen. Ist die weiße Kugel dabei, erhält der Spieler seinen Einsatz zurück. Bei zwei Kugeln mit gleicher Farbe erhält er vier Euro ausbezahlt. In allen anderen Fällen gibt es keine Auszahlung.Bestimmen Sie die Höhe des Einsatzes, so dass dieses Spiel fair ist.
(2,5 VP)
d) In einer anderen Urne befinden sich 200 schwarze und fünf rote Kugeln.Ein Spieler zieht 15-mal nacheinander eine Kugel und legt sie jeweils direkt wieder zurück. Er gewinnt, wenn er mindestens eine rote Kugel zieht. Berechnen Sie seine Gewinnwahrscheinlichkeit.
Dem Spieler wird folgendes Angebot gemacht. Er kann auf Züge verzichten, dafür werden weitere rote Kugeln in die Urne gelegt. Der Spieler muss vor dem Ziehen erklären, auf wie viele Züge er verzichtet. Für jeden weggelassenen Zug werden zwei rote Kugeln zusätzlich in die Urne gelegt.
Geben Sie einen Term an, mit dem die Gewinnwahrscheinlichkeit in Abhängigkeit von der Zahl x der weggelassenen Züge berechnet werden kann.
Ermitteln Sie auf wie viele Züge er verzichten muss, damit seine Gewinnwahrscheinlichkeit am größten ist.
(3 VP)
| Downloads |
PowerPoint